| 年级 | 科目 | 问题描述 | 提问时间 |
| 高二 | 数学 | 函数 | 2015-10-17 20:03:06 |
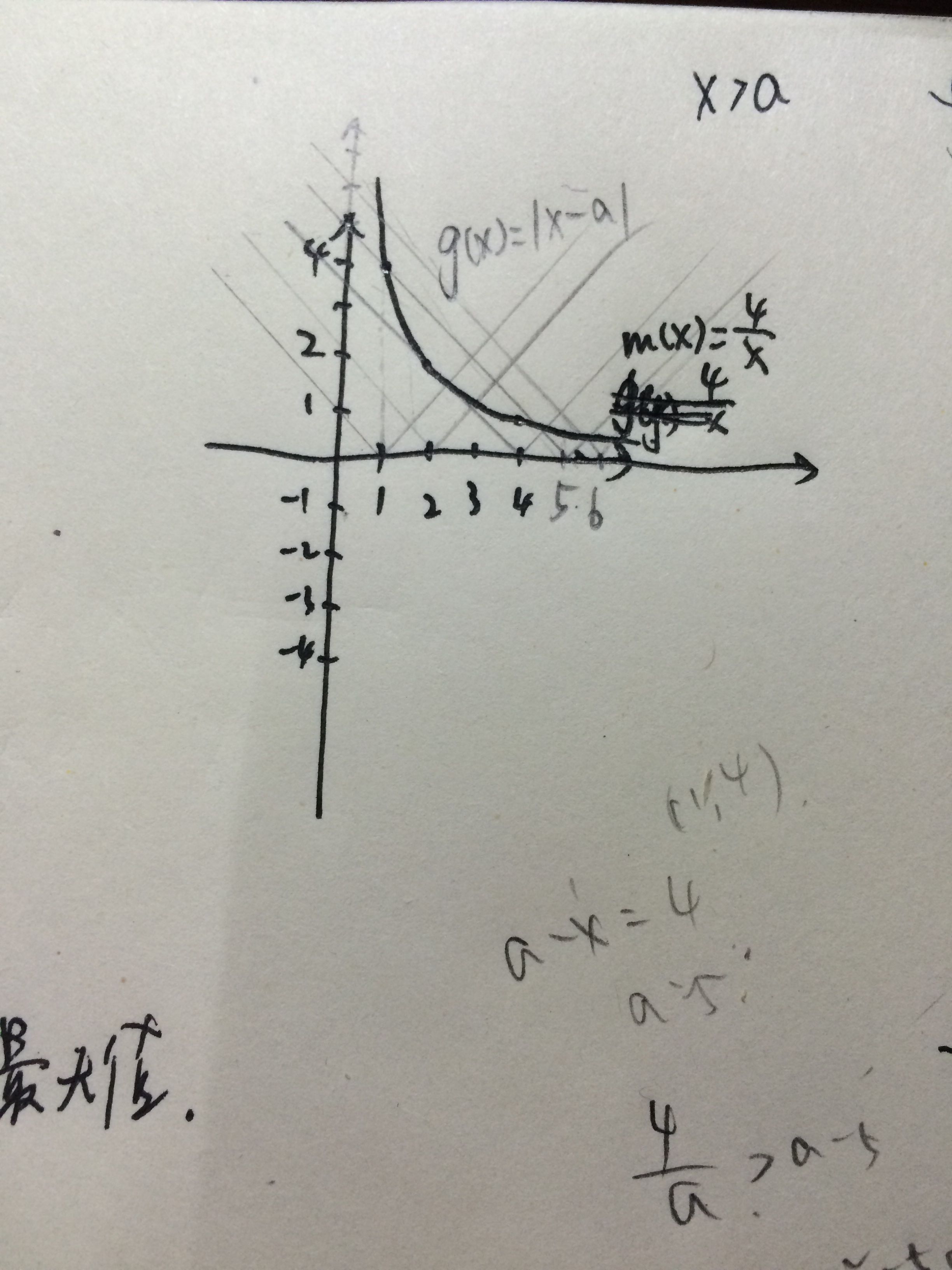
设f(x)=|x-a|-4/x,x∈[1,6],a∈(1,6). (1)若a∈(1,2],求f(x)的单调区间 (2)求f(x)的最小值
| |||
| 曾沛渝老师 2015-10-17 22:13:07 | |||
|
解:(Ⅰ)首先f(x)=2a-(x+4x),1≤x≤ax-4x,a<x≤6
因为当1<a≤2时,f(x)在[1,a]上是增函数,在[a,6]上也是增函数. 所以当1<a≤2时,y=f(x)在[1,6]上是增函数; (Ⅱ)①当1<a≤2时,由(Ⅰ)知,f(x)min=f(1)=2a-5, ②当2<a<6时,f(x)在[1,2]上是增函数,在[2,a]上是减函数,在[a,6]上是增函数. 又f(1)=2a-5,f(a)=a-4a ,且f(1)-f(a)=a+4a-5>0,解得4<a<6 所以当2<a<4时,f(x)min=f(1)=2a-5, 当4≤a<6时,f(x)min=f(a)=a-4a . 综上可知,f(x)min= 2a-5,1<a<4a-4a,4≤a<6 . | |||
| 学点点周老师 2015-10-17 22:18:43 | |||
 | |||
| 学点点周老师 2015-10-17 22:19:02 | |||
 | |||
| 学点点周老师 2015-10-17 22:46:15 | |||
| 不好意思同学,张老师把题目看错了哦,请参考雪老师的答案。 | |||